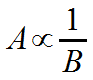Inverse Proportion and The Hyperbola Graph

Back Forces Physics Mathematics Contents Index Home

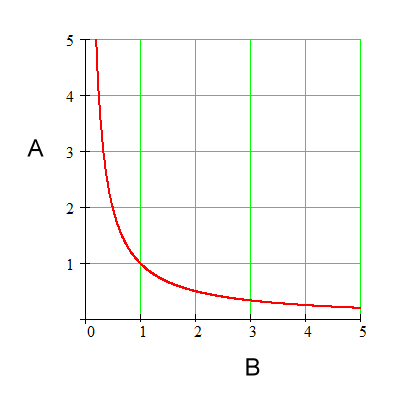
Hyperbola graphs, like the one immediately below, show that the quantities on the graph are in inverse proportion. This graph states, therefore, that A is inversely proportional to B. (It also states that B is inversely proportional to A, but we are going to work with the statement 'A is inversely proportional to B'.)

For the above graph:

This is how you write an inverse proportion. The symbol in the middle is the Greek letter alpha. It reads: A is inversely proportional to B. It means: By whatever factor A changes, B changes by the inverse of that factor. (Or you could say, “by the reciprocal of that factor”.)

 

Well, let's examine the graph and find out if its shape is such that A and B change by inverse factors.

Below is an example of a point on this graph. The point is (B1, A1) and it has coordinates (1, 1).

For the above graph:

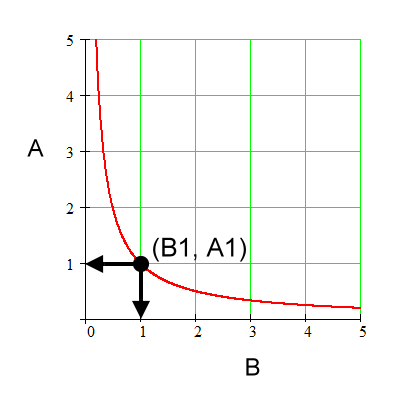
	Coordinate for B1.
	Coordinate for A1.

 

We will check for this hyperbola shape of a graph if we change A by some factor, does B truly change by the inverse factor, thus showing that this hyperbola shape represents an inverse proportion.

Here's what we are looking for:

 

The explanation:

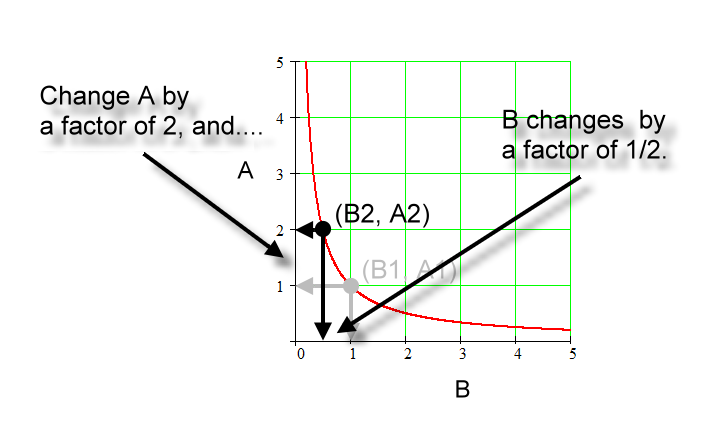
In the graph below we go from 'sub 1' to 'sub 2' and change the quantity A by a factor of 2; that is, we double it.

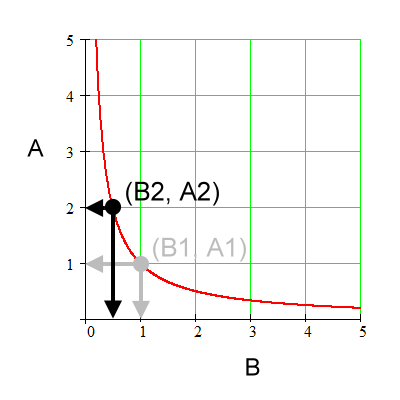
For the above graph:

	Coordinates for (B1, A1).
	Coordinates for (B2, A2).
	Going from 'sub 1' to 'sub 2', A changes by a factor of 2. That is, A1 times a factor of 2 equals A2.
	Going from 'sub 1' to 'sub 2' B, changes by a factor of 1/2. B1 times a factor of 1/2 equals B2.
	A and B change by the inverse factors. Those factors are 2 and ½ respectively.
	Therefore, A is inversely proportional to B.

 

So, again:

Let's try this again below for another point using the same graph. Here's where we are headed:

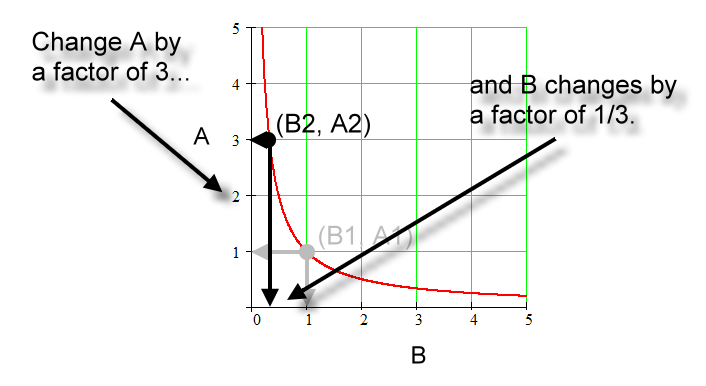
The steps follow as we move from 'sub 1' to 'sub 2':

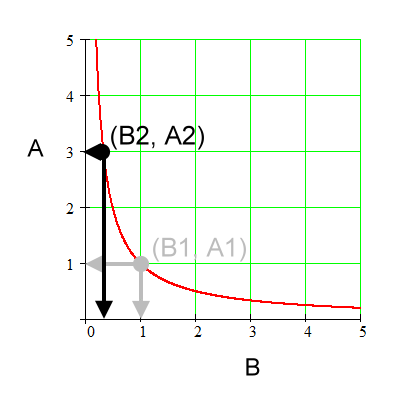
For the above graph:

	Coordinates for (B1, A1).
	Coordinates for (B2, A2).
	Going from 'sub 1' to 'sub 2', A changes by a factor of 3.
	Going from 'sub 1' to 'sub 2', B changes by a factor of 1/3.
	A and B change by inverse factors. Those factors are 3 and 1/3 respectively.
	Therefore, A is inversely proportional to B.

 

Here's the picture once more:

And again, if A is inversely proportional to B, then B is inversely proportional to A. The logic works out the same.

 

The function on the graph is:

 

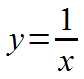
Or, using a formal function definition:

 

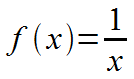
Lastly, this:

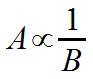
could probably be read 'A is directly proportional to the inverse of B', but that would be unusual. It's 'A is inversely proportional to B'.

 

Related:

Direct proportions

Linear functions

Inverse proportions

Direct proportion graph

Rational functions, 1/x

Back Forces Physics Mathematics Contents Index Home