Linear Functions and Equations
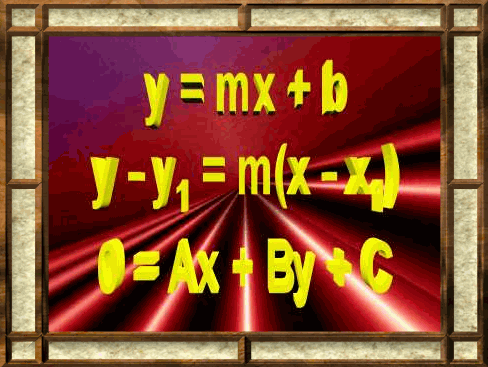
|
Linear functions are functions that have x as the input variable, and x has an exponent of only 1. Such functions look like the ones in the graphic to the left. Notice that x has an exponent of 1 in each equation. Functions such as these yield graphs that are straight lines, and, thus, the name linear. Linear functions come in three main forms. An explanation and animation are available for each by clicking the links below. |
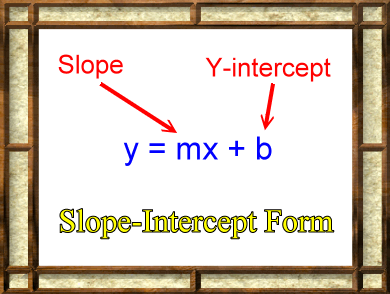 Slope-Intercept Form |
A very common way to express a linear function is named the 'slope-intercept form' of a linear function. When drawn on a common (x, y) graph it is usually expressed as: y = mx + b Or, in a formal function definition: f(x) = mx + b Basically, this function describes a set, or locus, of (x, y) points, and these points all lie along a straight line. The variable m holds the slope of this line. The variable b holds the y-coordinate for the spot where the line crosses the y-axis. This point is called the 'y-intercept'. Click the picture or the link to go on. |
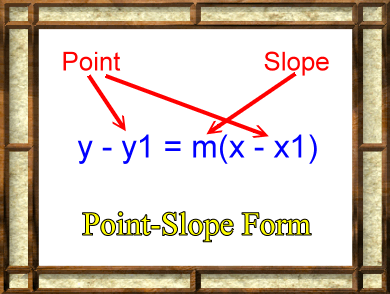 Point-Slope Form |
Technically, one should probably say that the picture to the left shows the 'point-slope form' for the equation of a line. The statement does not start with 'y =' or 'f(x)=', so it's not written in a common function definition form. That's not too hard to do, though, with a bit of algebra: y = m(x - x1) + y1 Or, as a formal function definition: f(x) = m(x - x1) + y1 So where in the equation is the point and the slope of the line? The variable m is the slope of the line and the point (x1, y1) is a known point on the line. If you know the slope of and the coordinates for one point on the line, then you could enter those values into this equation, and the equation would then define a set, or locus, of all the points on that line. Click the picture or the link to go on. |
 General Form |
To the left is the 'general form' for the equation of a line. Basically, A, B, and C are three numbers. So the equation could look like this: 0 = 2x + 3y + 4 As it turns out, all the points with (x, y) coordinates that would make the above statement true form a line. Using algebra, this general form can be changed into a slope-intercept form, and then you would know the slope and y-intercept for the line. Click the picture or the link to go on. |